research

\(\blacktriangleright\) Research interests: information scrambling, quantum chaos, dual-unitary circuits; tensor networks and Trotter simulations; quantum error correction (group-covariant codes); operator algebras and fragmentation; quantum algorithms (quantum signal processing, qubitization), quantum error mitigation for NISQ-hardware; randomized benchmarking and unitary designs for qudits; classical shadow tomography.

Information scrambling and quantum chaos

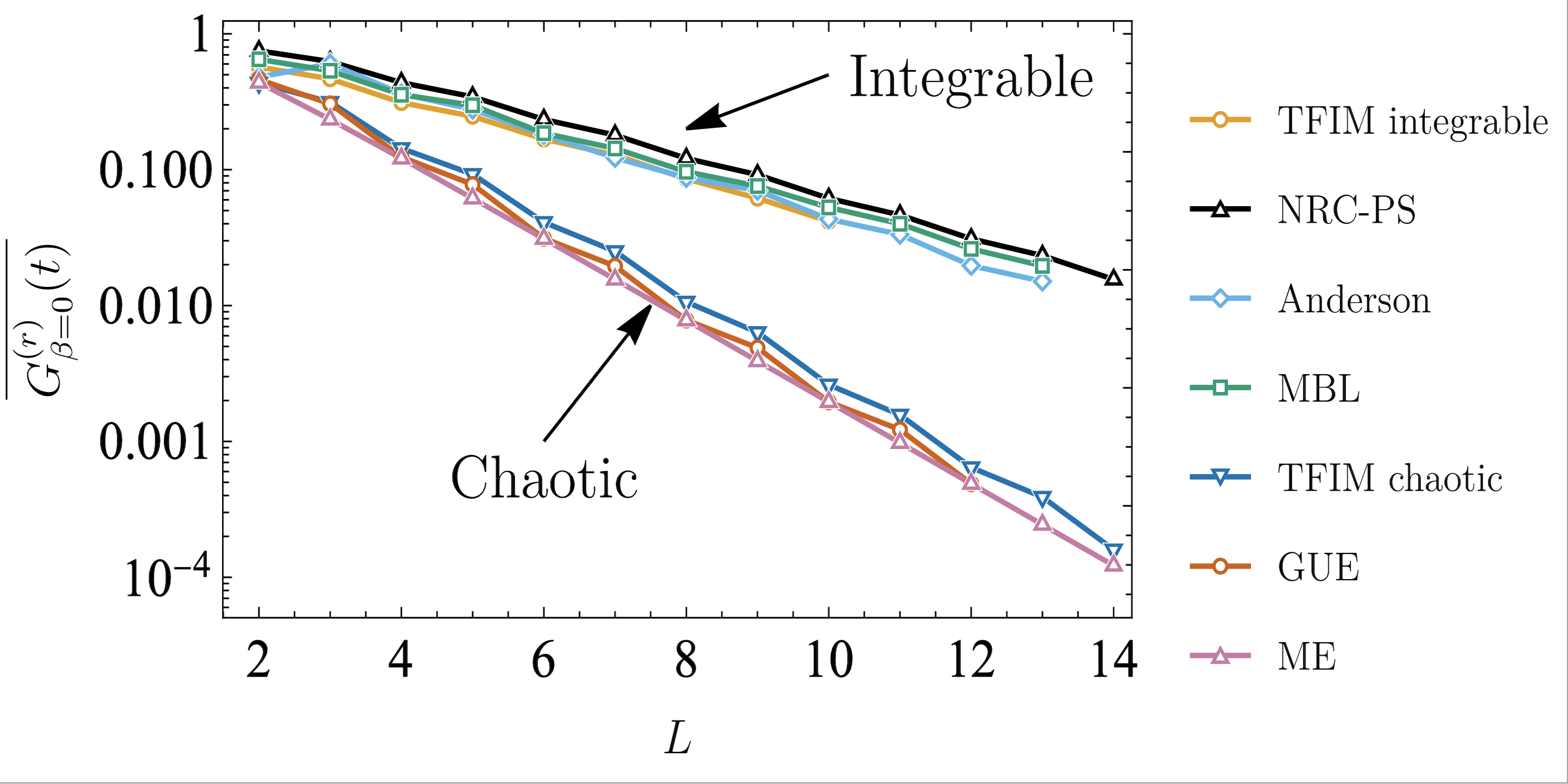
Symmetry is perhaps the most powerful principle in all of physics. And this remains true even in the quantum realm where systems with ‘quasi-local symmetries’ are distinguished from those without. This classification goes under a more familiar name, that of integrable versus non-integrable (a.k.a. chaotic) models. Quantum systems that are integrable generate “exactly solvable” dynamics and no quantum advantage can be obtained from these. In this sense, this is not only a fundamental, rather a practical problem. However, given a Hamiltonian, it is not always easy to classify whether it is integrable or chaotic. Ideally, by simply ‘looking’ at the dynamics, one should be able to tell them apart. Unfortunately, this is rarely the case. For example, it is known that quenched entanglement cannot distinguish these two models. Over the years, several quantities such as ‘out-of-time-ordered correlators’ (OTOCs) and ‘operator space entanglement’ have been introduced to identify these phases. OTOCs were famously used to understand how information is scrambled in models of black holes. In (Styliaris et al., 2021) we showed that nonlocal (OTOCs) are exactly equal to the operator space entanglement of quantum many-body dynamics. While it was unclear if OTOCs are good for detecting quantum chaos in systems with locality, our work established a connection between OTOCs and operator entanglement. We then utilized operator entanglement to show that the ‘equilibration value’ of operator entanglement is a robust quantifier of non-integrability. This was one of the first rigorous connections between OTOCs and entanglement, which also clarified why OTOCs are related to ‘operator space entanglement’ and not ‘state-space entanglement’.

Quantum superposition and entanglement are widely believed to be the two fundamental ingredients that distinguish quantum systems from their classical counterparts. While deep connections between entanglement and quantum ergodicity have been established over the years, our work in (Styliaris et al., 2019) provided the first rigorous connections (both analytical and numerical) between quantum superposition and ergodicity/thermalization. Using tools from the resource theory of coherence, we showed that the amount of superposition in a quantum state (with respect to a reference basis) can be used to detect whether the dynamics is localized (and hence will escape thermalization). Building upon this, in (Anand et al., 2021), we showed that quantum superposition with respect to the Hamiltonian eigenbasis can detect “eigenstate phase transitions” such as the ergodic-to-localization transitions and the transition from integrability-to-chaos. An open problem here is to generalize these connections to the more exotic phenomena of Hilbert-space fragmentation and quantum many-body scars.

Qudits

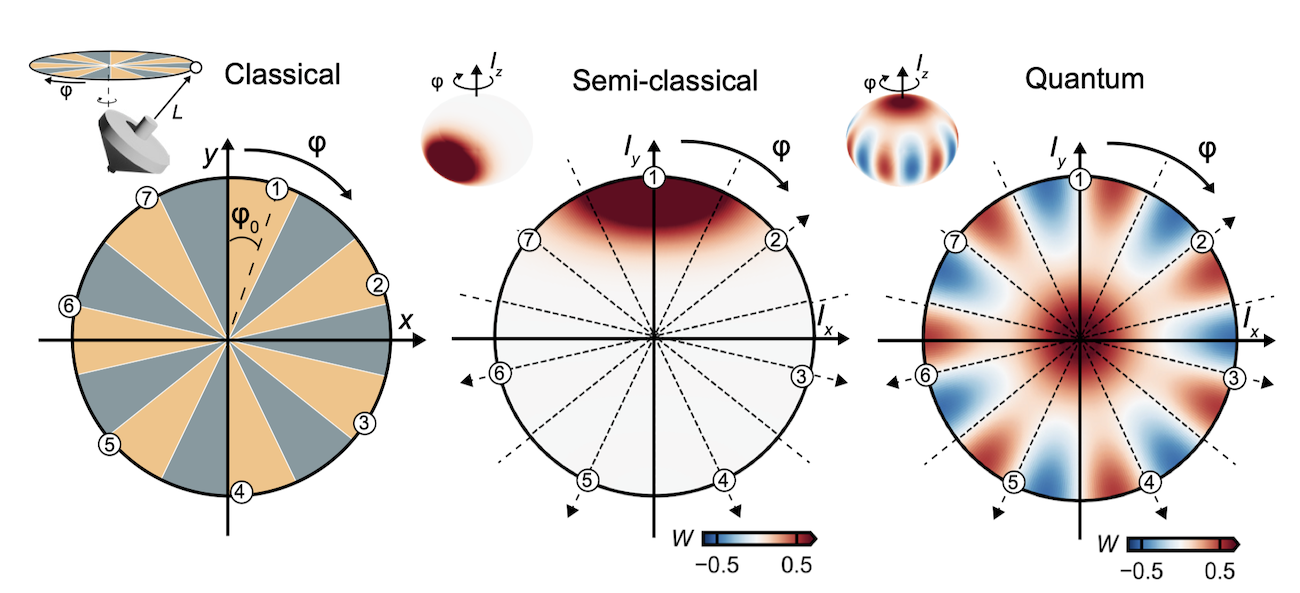
While qubits have been the traditional building-block for quantum computers for over two decades now, there is renewed interest in understanding the computational advantage offered by qudit platforms. Intuitively, qudits allow us to get more “bang for our buck” in terms of encoding more quantum information in a single unit. However, they are not without their own challenges. One of these challenges is that many quantum information primitives only work well for qudits with dimensions that are prime-power. A striking example is that there are no ‘unitary t-groups’ for non-prime power dimensions (such as d=6,10,14, and so on). A consequence of this is that the beloved Clifford group is no longer as useful for qudits as it is for qubits, e.g., one cannot twirl away an arbitrary noise channel with them. As a result, many of the standard techniques such as randomized benchmarking, classical shadow tomography, etc. no longer work in a straightforward way for qudits. In an upcoming work, we introduced a class of ‘weighted’ unitary designs that actively mitigate this issue for arbitrary dimensions (and reduce to standard Clifford group designs when the dimension is prime-power). This has allowed us to introduce a ‘native’ benchmarking scheme for cavity-QED systems where these standard techniques fail. In collaboration with Andrea Morello’s group at UNSW, I also worked on experimentally preparing and verifying ‘cat-states’ for spin qudits in (Yu et al., 2025). These states are the logical states for a ‘spin-GKP’ encoding that allows us to encode a logical qubit in an 8-dimensional qudit. We also utilized this Antimony qudit hardware to experimentally certify the ‘quantumness’ of nonclassical states using precession protocols in (Vaartjes et al., 2025).

Quantum applications

Dynamical decoupling is the cheapest form of quantum error suppression available to quantum hardware today. Building on some of my past work (Pokharel et al., 2018) where we demonstrated the utility of dynamical decoupling sequences in error suppression, we’re developing native DD schemes for various qudit platforms.

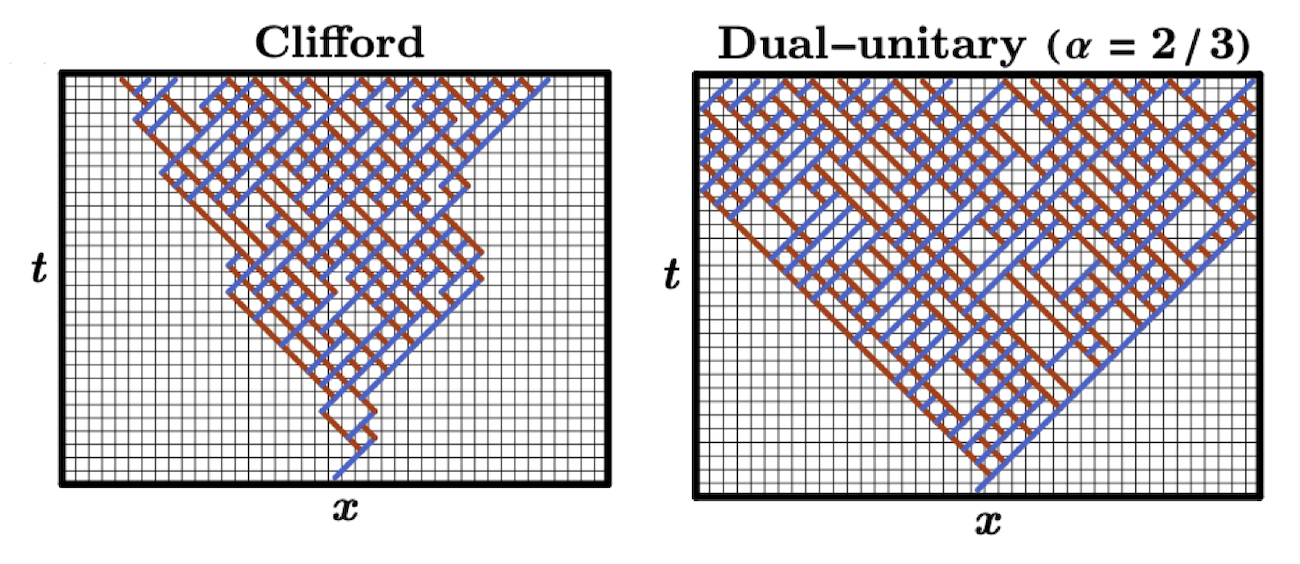
Classical shadow tomography is a protocol to learn many features of quantum states without incurring the exponential cost associated with full tomography. The state-of-the-art method utilizes classical shadows constructed from random Clifford circuits and is known to be optimal. However, in our recent work, we showed that another exactly solvable class of quantum dynamics, so-called ‘dual-unitary’ quantum circuits, can be utilized to introduce a shadow tomography scheme (Akhtar et al., 2024). These quantum circuits are the only local quantum dynamics that is provably quantum chaotic. They are also the ‘fastest scramblers’ of local quantum information and have found use in many exotic areas of physics such as modeling black hole phenomena. In our work, we showed that dual-unitary shadow tomography (‘DUST’) outperforms standard Clifford shadows when predicting observables with nearly full support. In fact, if we restrict to finite-depth quantum circuits, which is the only feasible scheme in the NISQ-era, DUST beats Clifford shadows at every circuit depth. Moreover, this advantage is not asymptotic, rather, it is even larger for small system sizes (number of qubits). An interesting future direction is to utilize these dual-unitary circuits for benchmarking quantum devices since they can form unitary designs at the fastest possible rates amongst all two-qubit unitaries.

Quantum optics

One of my key interests is in understanding the limits of quantum computers, perhaps most famously captured by the Gottesman-Knill theorem which showed that quantum circuits consisting solely of Clifford unitaries can be efficiently simulated on a classical computer. This is surprising at first glance since one can generate highly entangled states with Clifford unitaries. This theorem also breaks the blanket understanding of entanglement as the limiting factor for quantum simulation. In fact, every well-behaved quantum resource inspires its own notion of computational complexity. In (Marshall & Anand, 2023) we introduced a scheme to simulate continuous-variable (CV) systems. We showed how to systematically approximate any CV state as a linear combination of finitely many coherent states. The cost of classical simulation boils down to two independent contributions: the number of single-photon additions and the amount of squeezing. This work showed that in CV systems, non-Gaussianity is the equivalent resource to ‘magic’ in qubits.

Fault-tolerant linear optical quantum computation relies on interference between identical photons to generate entanglement. Unfortunately, photons in the lab tend to be partially distinguishable, generating less entanglement and causing unheralded errors. In (Saied et al., 2025) we introduced families of distillation schemes that use n-photon interference and postselection to filter out “bad” photons and reduce distinguishability by a factor of n, with resource costs scaling only linearly in n. Along the way, the team also resolves an open problem regarding n-mode Fourier interferometers, namely that the Zero Transmission Law characterizes all suppression if and only if n is a prime power.